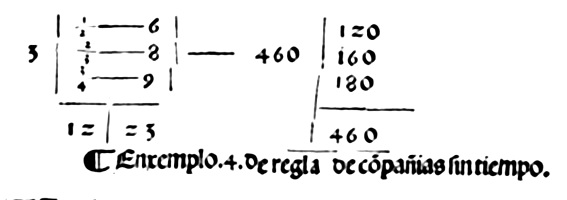regla
|
1. sust.
f.
1ª datación del corpus: Sánchez de las Broças, Helt Frisio, Relox español, 1549.
Marca diatécnica:
Geom.
Definición:Instrumento de madera, metal u otra materia rígida, por lo común de poco grueso y de forma rectangular, que sirve principalmente para trazar líneas rectas, o para medir la distancia entre dos puntos. (DRAE 2001).Ejemplo(s):
|
|
2. sust.
f.
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Arq.
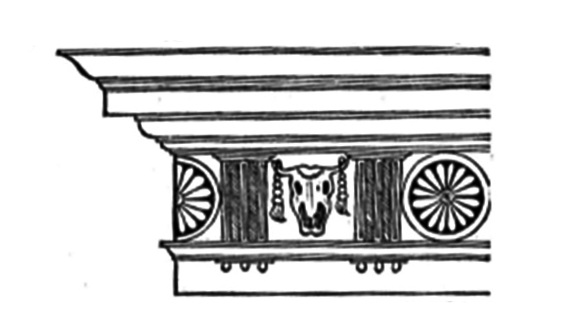
Definición:Moldura plana de la que penden las gotas bajo el triglifo en el entablamento dórico.Ejemplo(s):
|
|
3. sust.
f.
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Metod.
Definición:Precepto, principio o axioma en las ciencias o artes. (Autoridades).Ejemplo(s):
|
|
4. sust.
f.
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Arit.
Definición:Método de hacer una operación. (DRAE 2001).Ejemplo(s):
|
|
~ alta
1ª datación del corpus: López de Arenas, Reglas de la carpintería, 1619.
Marca diatécnica:
Carp. bl.
Definición:Longitud de la quiebra del faldón con el almizate. (Nuere, Carpintería).Ejemplo(s):
|
|
~ baja
1ª datación del corpus: López de Arenas, Reglas de la carpintería, 1619.
Marca diatécnica:
Carp. bl.
Definición:Longitud del faldón en la cinta del almarbate. (Nuere, Carpintería).Ejemplo(s):
|
|
~ de compañía
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Arit.
Definición:La que enseña a dividir una cantidad en partes proporcionales a otras cantidades conocidas, empleada principalmente para la distribución de ganancias o pérdidas entre los socios de una compañía comercial con arreglo a los capitales aportados por cada uno. (DRAE 2001).Ejemplo(s):
Información enciclopédica:"Este tipo de cuestiones aparecieron por primera vez en los textos de Aritmética a finales de la Edad Media. Los mercaderes y banqueros, que comenzaban a tener importancia como parte de la naciente burguesía, necesitaban saber cómo llevar las cuentas de sus negocios. Pensando en ellos se empezó a incluir en los libros de Aritmética problemas que tenían ya el enunciado clásico de la regla de compañía [...]. En un comienzo los problemas sobre la adjudicación de beneficios en un negocio no se distinguían de otras cuestiones sobre el reparto proporcional que se solían introducir como aplicaciones de la regla de tres [...]. Sólo al final de la Edad Media la regla de compañía comenzó a figurar habitualmente entre los problemas de repartos proporcionales, a distinguirse de otras cuestiones similares y a conocerse por su nombre" (Navarro Loidi, J., 2006, "La regla de compañía y la didáctica del reparto proporcional", Sigma, 28, p. 117). "Para resolver la regla de compañía se divide la ganancia o pérdida total en partes proporcionales a los capitales, si estos han estado impuestos el mismo tiempo; y en partes proporcionales a los productos de cada capital por su tiempo, cuando no han estado impuestos el mismo tiempo" (Picatoste y Rodríguez, F., 1861, Principios y ejercicios de Aritmética y Geometría, pp. 88-89). "Esta regla tiene por objeto hallar la ganancia o pérdida que corresponde a cada uno de los socios, conociendo la ganancia o pérdida total. Estas ganancias o pérdidas individuales son proporcionales directamente a los capitales impuestos y al tiempo que han estado impuestos. Se llama simple o sin tiempo cuando todos los capitales han estado impuesto un mismo tiempo; y compuesta o con tiempo en el caso contrario" (Picatoste y Rodríguez, F., 1862, Vocabulario matemático-etimológico, p. 103). |
|
~ de compañía llana
1ª datación del corpus: Aurel, Arithmética algebrática, 1552.
Marca diatécnica:
Arit.
Definición:La que enseña a dividir una cantidad en partes proporcionales a otras cantidades conocidas, empleada principalmente para la distribución de ganancias o pérdidas entre los socios de una compañía comercial con arreglo a los capitales aportados por cada uno durante un mismo periodo de tiempo.Sinónimos(s):regla de compañía(s) simple, regla de compañía sin tiempo.Antónimos(s):regla de compañía(s) con tiempo, regla de compañía mixta.Ejemplo(s):
|
|
~ de compañía mixta
1ª datación del corpus: Pérez de Moya, Arithmética práctica, 1562.
Marca diatécnica:
Arit.
Definición:La que enseña a dividir una cantidad en partes proporcionales a otras cantidades conocidas, empleada principalmente para la distribución de ganancias o pérdidas entre los socios de una compañía comercial con arreglo a los capitales aportados por cada uno en distintos periodos de tiempo.Sinónimos(s):regla de compañía(s) con tiempo.Antónimos(s):regla de compañía llana, regla de compañía(s) simple, regla de compañía sin tiempo.Ejemplo(s):
|
|
~ de compañía sin tiempo
1ª datación del corpus: Pérez de Moya, Arithmética práctica, 1562.
Marca diatécnica:
Arit.
Definición:La que enseña a dividir una cantidad en partes proporcionales a otras cantidades conocidas, empleada principalmente para la distribución de ganancias o pérdidas entre los socios de una compañía comercial con arreglo a los capitales aportados por cada uno durante un mismo periodo de tiempo.Sinónimos(s):regla de compañía llana, regla de compañía(s) simple.Antónimos(s):regla de compañía(s) con tiempo, regla de compañía mixta.Ejemplo(s):
|
|
~ de compañía(s) con tiempo
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Arit.
Definición:La que enseña a dividir una cantidad en partes proporcionales a otras cantidades conocidas, empleada principalmente para la distribución de ganancias o pérdidas entre los socios de una compañía comercial con arreglo a los capitales aportados por cada uno en distintos periodos de tiempo.Sinónimos(s):regla de compañía mixta.Antónimos(s):regla de compañía llana, regla de compañía(s) simple, regla de compañía sin tiempo.Ejemplo(s):
|
|
~ de compañía(s) simple
1ª datación del corpus: Pérez de Moya, Arithmética práctica, 1562.
Marca diatécnica:
Arit.
Definición:La que enseña a dividir una cantidad en partes proporcionales a otras cantidades conocidas, empleada principalmente para la distribución de ganancias o pérdidas entre los socios de una compañía comercial con arreglo a los capitales aportados por cada uno durante un mismo periodo de tiempo.Sinónimos(s):regla de compañía llana, regla de compañía sin tiempo.Antónimos(s):regla de compañía(s) con tiempo, regla de compañía mixta.Ejemplo(s):
|
|
~ de la cantidad
1ª datación del corpus: Aurel, Arithmética algebrática, 1552.
Marca diatécnica:
Álg.
Definición:La que enseña a resolver sistemas de ecuaciones lineales de dos o más incógnitas.Ejemplo(s):
Información enciclopédica:"The rule of quantity or the rule of the second quantity are the expressions used in the first treatises on algebra to refer to a procedure of solving problems in which more than one unknown were involved. The first appearance of the second unknown in Western culture was probably around 1373 in the Trattato di Fioretti by Antonio de Mazzinghi. The use of more than one unknown would lead to the solution of simultaneous linear equations, whose discussion represented a big step forward in the process of algebraization of mathematics [...]. The method to solve these problems consists in putting the second unknown in terms of the first one, the same for the third unknown, and so on. X being the first unknown, he puts q for the second unknown, and when the second is expressed in terms of the first he also puts q for the third, and so on" (Romero Vallhonesta, F., 2011, The “rule of quantity” in spanish algebras ofthe 16th century. Possible sources, pp. 94-96). |
|
~ de la cantidad absoluta
1ª datación del corpus: Núñez, Álgebra en Arithmética, 1567.
Marca diatécnica:
Álg.
Definición:La que enseña a resolver sistemas de ecuaciones lineales de dos o más incógnitas.Ejemplo(s):
|
|
~ de la cantidad simple
1ª datación del corpus: Núñez, Álgebra en Arithmética, 1567.
Marca diatécnica:
Álg.
Definición:La que enseña a resolver sistemas de ecuaciones lineales de dos o más incógnitas.Ejemplo(s):
Información enciclopédica:"The author says that the rule of simple or absolute quantity is different from the others and that we use it in two ways. The first way [the rule os simple quantity] is a substitution of the rule of the thing to perform the equality with the help of the term quantity, while the second [the rule of absolute quantity] is to do «position» over «position». With this last expression, Núñez refers to problems whose wording contains one unknown, as we will see in the second problem of this chapter" (Romero Vallhonesta, F., 2011, The “rule of quantity” in spanish algebras ofthe 16th century. Possible sources, p. 106). |
|
~ de la cosa
1ª datación del corpus: Aurel, Arithmética algebrática, 1552.
Marca diatécnica:
Álg.
Definición:Parte de las matemáticas en la cual las operaciones aritméticas son generalizadas empleando números, letras y signos. Cada letra o signo representa simbólicamente un número u otra entidad matemática. Cuando alguno de los signos representa un valor desconocido se llama incógnita. (DRAE, s.v. álgebra).Ejemplo(s):
|
|
~ de la segunda cosa
1ª datación del corpus: Aurel, Arithmética algebrática, 1552.
Marca diatécnica:
Álg.
Definición:La que enseña a resolver sistemas de ecuaciones lineales de dos o más incógnitas.Ejemplo(s):
Información enciclopédica:En la obra de Luca Pacioli, Summa de arithmetica geometria proportioni et proportionalitá (1494), "he calls the unknowns surd quantities [cantidades o números irracionales] and he proposes to call the first co. and the second quantita" (Romero Vallhonesta, F., 2011, The “rule of quantity” in spanish algebras ofthe 16th century. Possible sources, p. 97). |
|
~ de tres
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Arit.
Definición:La que enseña a determinar una cantidad desconocida por medio de una proporción de la cual se conocen dos términos entre sí homogéneos, y otro tercero de la misma especie que el cuarto que se busca. (DRAE 2001).Ejemplo(s):
|
|
~ de tres con tiempo
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Arit.
Definición:La que enseña a determinar una cantidad desconocida por medio de una proporción de la cual se conocen más de tres términos entre sí distintos, referidos principalmente a las cantidades o valor de monedas y al tiempo que las mismas han servido.Sinónimos(s):regla de tres mixta.Antónimos(s):regla de tres llana, regla de tres simple, regla de tres sin tiempo.Ejemplo(s):
|
|
~ de tres cosas
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Arit.
Definición:La que enseña a determinar una cantidad desconocida por medio de una proporción de la cual se conocen dos términos entre sí homogéneos, y otro tercero de la misma especie que el cuarto que se busca. (DRAE, s. v. regla de tres).Ejemplo(s):
|
|
~ de tres llana
1ª datación del corpus: Aurel, Arithmética algebrática, 1552.
Marca diatécnica:
Arit.
Definición:La que enseña a determinar una cantidad desconocida por medio de una proporción de la cual se conocen tres términos entre sí distintos, referidos principalmente a las cantidades o valor de monedas, sin tener en cuenta el tiempo que las mismas han servido.Sinónimos(s):regla de tres simple, regla de tres sin tiempo.Antónimos(s):regla de tres con tiempo, regla de tres mixta.Ejemplo(s):
|
|
~ de tres mixta
1ª datación del corpus: Pérez de Moya, Arithmética práctica, 1562.
Marca diatécnica:
Arit.
Definición:La que enseña a determinar una cantidad desconocida por medio de una proporción de la cual se conocen más de tres términos entre sí distintos, referidos principalmente a las cantidades o valor de monedas y al tiempo que las mismas han servido.Sinónimos(s):regla de tres con tiempo.Antónimos(s):regla de tres llana, regla de tres simple, regla de tres sin tiempo.Ejemplo(s):
|
|
~ de tres simple
1ª datación del corpus: Pérez de Moya, Manual de contadores, 1589.
Marca diatécnica:
Arit.
Definición:La que enseña a determinar una cantidad desconocida por medio de una proporción de la cual se conocen tres términos entre sí distintos, referidos principalmente a las cantidades o valor de monedas, sin tener en cuenta el tiempo que las mismas han servido.Sinónimos(s):regla de tres llana, regla de tres sin tiempo.Antónimos(s):regla de tres con tiempo, regla de tres mixta.Ejemplo(s):
|
|
~ de tres sin tiempo
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Arit.
Definición:La que enseña a determinar una cantidad desconocida por medio de una proporción de la cual se conocen tres términos entre sí distintos, referidos principalmente a las cantidades o valor de monedas, sin tener en cuenta el tiempo que las mismas han servido.Sinónimos(s):regla de tres llana, regla de tres simple.Antónimos(s):regla de tres con tiempo, regla de tres mixta .Ejemplo(s):
|
|
~ de(l) álgebra
1ª datación del corpus: Aurel, Arithmética algebrática, 1552.
Marca diatécnica:
Álg.
Definición:Parte de las matemáticas en la cual las operaciones aritméticas son generalizadas empleando números, letras y signos. Cada letra o signo representa simbólicamente un número u otra entidad matemática. Cuando alguno de los signos representa un valor desconocido se llama incógnita. (DRAE, s. v. álgebra).Ejemplo(s):
|
|
~ de(l) calibre
1ª datación del corpus: Ufano, Tratado de la Artillería, 1613.
Marca diatécnica:
Art.
Definición:Instrumento formado por una regla o plantilla graduadas con que se indica el peso de las balas a partir de su diámetro.Ejemplo(s):
|
|
~ del cos2
1ª datación del corpus: Pérez de Moya, Arithmética práctica, 1562.
Marca diatécnica:
Álg.
Definición:Parte de las matemáticas en la cual las operaciones aritméticas son generalizadas empleando números, letras y signos. Cada letra o signo representa simbólicamente un número u otra entidad matemática. Cuando alguno de los signos representa un valor desconocido se llama incógnita. (DRAE, s. v. álgebra).Sinónimos(s):álgebra, almucábala, Arte Mayor, Regla de(l) álgebra, Regla de la cosa, Reglas reales.Ejemplo(s):
|
|
~ estatus
1ª datación del corpus: Rojas, Compendio fortificación, 1613.
Marca diatécnica:
Geom.
Definición:Instrumento para medir distancias, alturas y profundidades, construyendo triángulos semejantes.Ejemplo(s):
|
|
~ extraordinaria
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Arit.
Definición:Método no común ni usual de hacer una operación.Ejemplo(s):
|
|
~ fémur
1ª datación del corpus: Urrea, Vitruvio, Architectura, 1582.
Marca diatécnica:
Arq.
Definición:Banda plana vertical situada entre las canaladuras de los triglifos.Ejemplo(s):
|
|
~ general
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Arit.
Definición:Método común, frecuente y usual de hacer una operación.Ejemplo(s):
|
|
~ numeral
1ª datación del corpus: Ufano, Tratado de la Artillería, 1613.
Marca diatécnica:
Art.
Definición:Instrumento formado por una regla o plantilla graduadas con que se indica el peso de las balas a partir de su diámetro.Ejemplo(s):
|
|
~s reales
1ª datación del corpus: Pérez de Moya, Arithmética práctica, 1562.
Marca diatécnica:
Álg.
Definición:Parte de las matemáticas en la cual las operaciones aritméticas son generalizadas empleando números, letras y signos. Cada letra o signo representa simbólicamente un número u otra entidad matemática. Cuando alguno de los signos representa un valor desconocido se llama incógnita. (DRAE, s.v. álgebra).Sinónimos(s):álgebra, almucábala, Arte Mayor, Regla de(l) álgebra, Regla de la cosa, Regla del cos.Ejemplo(s):
|
|
las cuatro ~s
pl.
1ª datación del corpus: Aurel, Arithmética algebrática, 1552.
Marca diatécnica:
Arit.
Definición:Las cuatro operaciones de sumar, restar, multiplicar y dividir. (DLE).Ejemplo(s):
|
|
a ~ 1
1ª datación del corpus: Vandelvira, Traças de cortes, ca. 1591.
Marca diatécnica:
Cant.
Definición:Dicho de justificar o comprobar obras artificiales: Con ayuda de la regla. (DRAE 2001).Ejemplo(s):
|
|
a ~ 2
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Geom.
Definición:En derecho, en linea recta.Ejemplo(s):
|
|
a ~ y borneo
1ª datación del corpus: Martínez de Aranda, Zerramientos montea, ca. 1599.
Marca diatécnica:
Cant.
Definición:Con ayuda de la regla y mediante nivelación a ojo.Ejemplo(s):
Información enciclopédica:Técnica de labra de piedras en el que se obtiene una cara plana comprobando con una regla y la vista; esta cara se puede dejar plana, por ejemplo en un sillar, o después seguir la labra ahondando la pieza hasta conseguir una superficie curva (Calvo López: s. v. regla). |
|
a~ y escuadra
1ª datación del corpus: Rojas, Teórica fortificación, 1598.
Marca diatécnica:
Cant.
Definición:En línea recta y formando ángulos rectos mediante regla y escuadra.Ejemplo(s):
|
|
a ~ y nivel
1ª datación del corpus: Loçano, Alberto, Architectura, 1582.
Marca diatécnica:
Constr.
Definición:En línea recta y horizontalmente mediante regla y nivel.Ejemplo(s):
|
|
a ~ y plomo
1ª datación del corpus: Loçano, Alberto, Architectura, 1582.
Marca diatécnica:
Constr.
Definición:En línea recta y verticalmente mediante regla y plomada.Ejemplo(s):
|
<< Volver