<< Volver
<< Volver
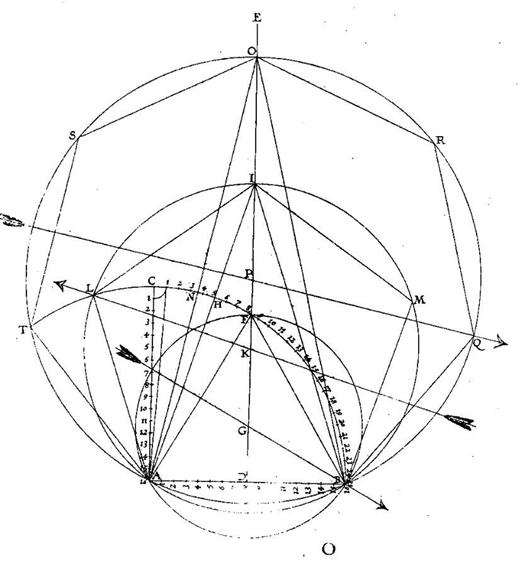
poligonio
(
tomado del lat.
pŏlygōnǐus, y este del griego πολυγώνιος
(Lewis – Short)
).
Familia léxica: ambligonio, centágono, cincuentágono, decágono, diagonal, diagonalmente, diagonio, diágono, dodecágono, heptágono, hexagonal, hexagónico, hexágono, isogonio, nonágono, octógono, ortogonal, ortogonalmente, ortogónicamente, ortogonio, ortógono, oxigonio, pentágono, poligónico, polígono, septágono, sexágono, tetragónico, tetrágono, trigonio, trígono, veintágono, veinticincágono.
|
1. sust.
m.
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:Porción de plano limitada por líneas rectas. (DLE, s. v. polígono).Ejemplo(s):
|
|
2. adj.
1ª datación del corpus: Urrea, Vitruvio, Architectura, 1582. Definición:Dicho de una figura, limitada por varios lados y ángulosEjemplo(s):
|
|
~ equilátero
1ª datación del corpus: Ondériz, Euclides, Perspectiva y especularia, 1584-85.
Marca diatécnica:
Geom.
Definición:El que tiene todos sus lados iguales.Ejemplo(s):
|
|
~ regular
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El que tiene todos sus lados y ángulos iguales.Ejemplo(s):
|
|
Véase cuerda ~a.
|
|
Véase figura ~a.
|
<< Volver