figura
|
1. sust.
f.
1ª datación del corpus: Urrea, Vitruvio, Architectura, 1582.
Marca diatécnica:
Arq.
Definición:Estatua o pintura que representa el cuerpo de un hombre o animal. (DRAE 2001).Ejemplo(s):
|
|
2. sust.
f.
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553 .
Marca diatécnica:
Geom.
Definición:Espacio cerrado de uno o muchos términos. (Autoridades).Ejemplo(s):
|
|
3. sust.
f.
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Geom.
Definición:Línea o conjunto de líneas con que se representa un objeto. (DRAE 2001).Ejemplo(s):
|
|
4. sust.
f.
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Arit.
Definición:Signo lingüístico o matemático con que se representa cada uno de los números que forman el sistema numeral romano o arábigo.Ejemplo(s):
|
|
~ circular
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Geom.
Definición:La de forma de círculo.Ejemplo(s):
|
|
~ circunscrita
1ª datación del corpus: Vandelvira, Traças de cortes, ca. 1591.
Marca diatécnica:
Geom.
Definición:La que está por afuera de su inscrita y sus lados tocan todos los ángulos de la inscrita: y si es círculo, su circunferencia pasa por todos sus ángulos. (Autoridades, s. v. ~ circunscripta).Ejemplo(s):
|
|
~ columnar
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:Figura sólida prolongada contenida entre dos bases planas, paralelas e iguales y delimitada por una superficie circular.Ejemplo(s):
|
|
~ cónica
1ª datación del corpus: Álaba, Perfeto capitán, 1590.
Marca diatécnica:
Geom.
Definición:La que tiene forma de cono.Ejemplo(s):
|
|
~ corpórea
1ª datación del corpus: Chaves, Sacrobosco, Sphera, 1545.
Marca diatécnica:
Geom.
Definición:Cuerpo sólido, objeto en que puede apreciarse las tres dimensiones principales, longitud, anchura y altura.Ejemplo(s):
|
|
~ cuadrilátera
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553 .
Marca diatécnica:
Geom.
Definición:La que tiene cuatro lados.Ejemplo(s):
|
|
~ cúbica
1ª datación del corpus: Chaves, Sacrobosco, Sphera, 1545.
Marca diatécnica:
Geom.
Definición:Sólido regular limitado por seis cuadrados iguales. (DRAE 2001).Ejemplo(s):
|
|
~ curvilínea
1ª datación del corpus: Vandelvira, Traças de cortes, ca. 1591.
Marca diatécnica:
Geom.
Definición:La que está formada por líneas curvas.Ejemplo(s):
|
|
~ geométrica
1ª datación del corpus: Pérez de Moya, Arithmética práctica, 1562.
Marca diatécnica:
Geom.
Definición:Línea o conjunto de líneas con que se representa un objeto. (DRAE, s.v. figura).Ejemplo(s):
|
|
~ inscrita
1ª datación del corpus: Vandelvira, Traças de cortes, ca. 1591.
Marca diatécnica:
Geom.
Definición:La que estando dentro de otra toca a la de afuera con todos sus ángulos. (Autoridades, s. v. ~ inscripta).Ejemplo(s):
|
|
~ irregular
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553 .
Marca diatécnica:
Geom.
Definición:La que tiene lados y ángulos desiguales.Ejemplo(s):
|
|
~ lenticular
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:La que tiene forma de lente o de óvalo.Ejemplo(s):
|
|
~ llana
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:Porción de plano cerrada por una línea o un conjunto de líneas en una misma superficie.Ejemplo(s):
|
|
~ maciza
1ª datación del corpus: Álaba, Perfeto capitán, 1590.
Marca diatécnica:
Geom.
Definición:Cuerpo sólido, objeto en que puede apreciarse las tres dimensiones principales, longitud, anchura y altura.Ejemplo(s):
|
|
~ molar
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:Cuerpo sólido circular, a manera de muela, cuyas basas son planas.Ejemplo(s):
|
|
~ oval
1ª datación del corpus: Chaves, Sacrobosco, Sphera, 1545.
Marca diatécnica:
Geom.
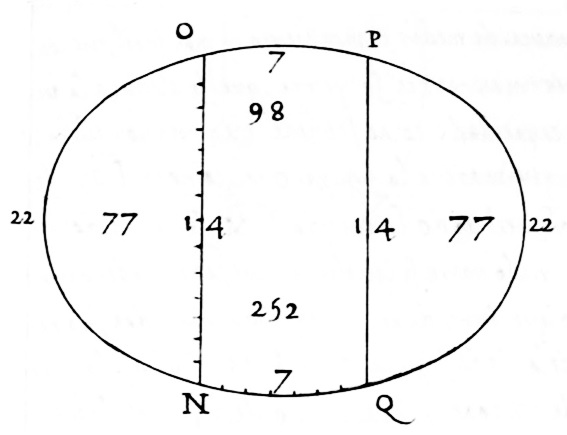
Definición:La que tiene forma de óvalo.Ejemplo(s):
|
|
~ plana
1ª datación del corpus: Chaves, Sacrobosco, Sphera, 1545.
Marca diatécnica:
Geom.
Definición:Porción de plano cerrada por una línea o un conjunto de líneas en una misma superficie.Ejemplo(s):
|
|
~ poligonia
1ª datación del corpus: Ondériz, Euclides, Perspectiva y especularia, 1584-85.
Marca diatécnica:
Geom.
Definición:La limitada por varios lados y ángulos.Ejemplo(s):
|
|
~ poligónica
1ª datación del corpus: Juanelo Turriano, Veinte y un libros, ca. 1605.
Marca diatécnica:
Geom.
Definición:La limitada por varios lados y ángulos.Ejemplo(s):
|
|
~ rectilínea
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:La que consta de líneas rectas.Ejemplo(s):
|
|
~ redonda
1ª datación del corpus: Chaves, Sacrobosco, Sphera, 1545.
Marca diatécnica:
Geom.
Definición:La que tiene forma circular.Ejemplo(s):
|
|
~ regular
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:La que tiene lados y ángulos iguales.Ejemplo(s):
|
|
~ sólida
1ª datación del corpus: Chaves, Sacrobosco, Sphera, 1545.
Marca diatécnica:
Geom.
Definición:Cuerpo sólido, objeto en que puede apreciarse las tres dimensiones principales, longitud, anchura y altura.Ejemplo(s):
|
|
~ superficial
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:Porción de plano cerrada por una línea o un conjunto de líneas en una misma superficie.Ejemplo(s):
|
|
simple ~
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:La que se contiene dentro de un límite, o que está comprendida por una línea curva.Ejemplo(s):
|
<< Volver