trapecio
|
1. adj.
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
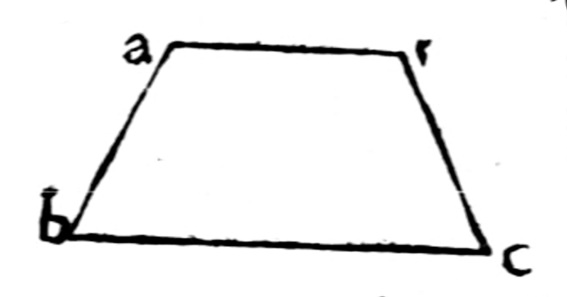
Definición:Dicho de un polígono: que tiene forma de cuadrilátero irregular, sin ningún lado paralelo a otro.Ejemplo(s):
|
|
2. sust.
m.
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
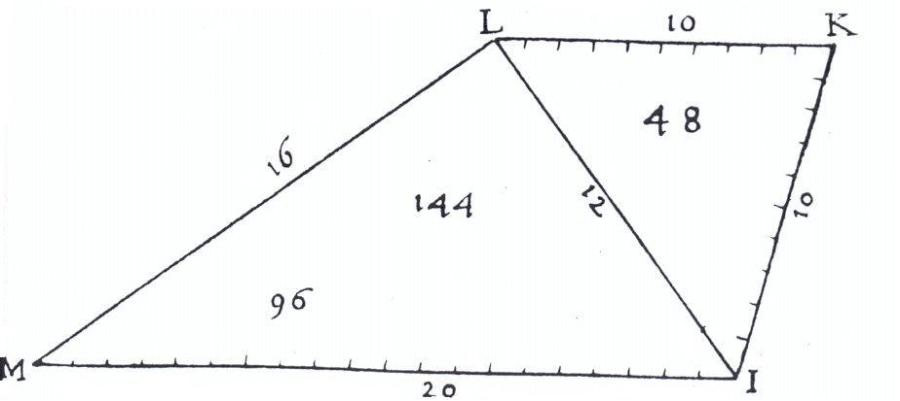
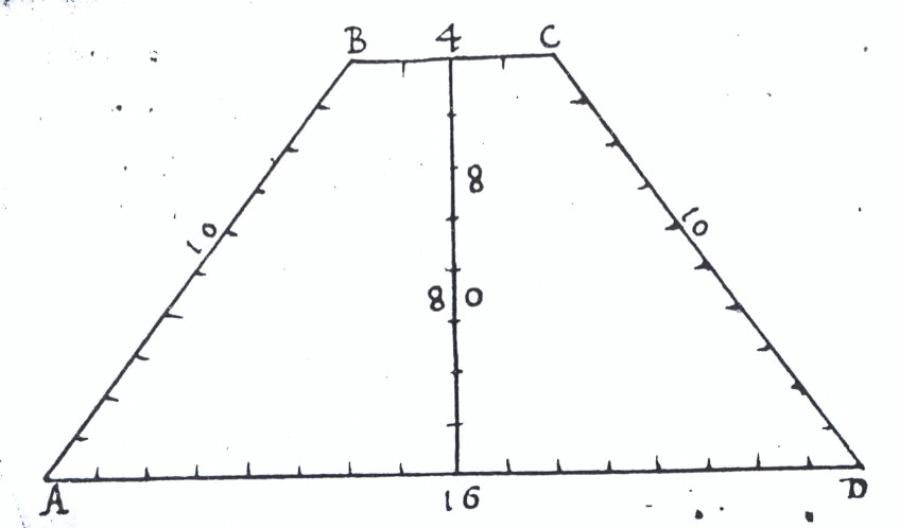
Definición:Cuadrilátero irregular que tiene paralelos solamente dos de sus lados. (DLE).Ejemplo(s):
|
|
~ ambligonio
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El que no tiene lados iguales ni ángulos rectos.Ejemplo(s):
|
|
~ isósceles
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El que tiene iguales los lados no paralelos.Ejemplo(s):
|
|
~ rectángulo
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El que tiene dos ángulos rectos.Ejemplo(s):
|
|
Véase columna ~a.
|
<< Volver