lado
|
1. sust.
m.
1ª datación del corpus: Sagredo, Medidas Romano, 1526. Definición:Cada una de las partes que limitan un todo (DLE).Ejemplo(s):
|
|
2. sust.
m.
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:Cada una de las dos líneas que forman un ángulo. (DLE).Ejemplo(s):
|
|
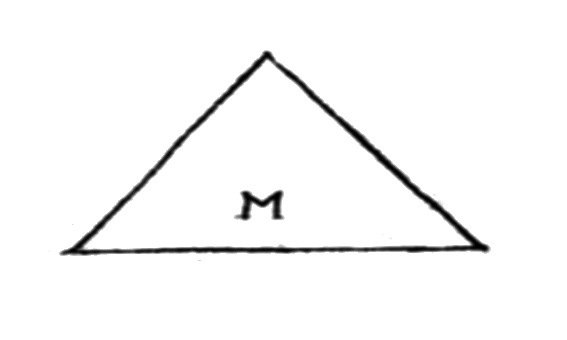
3. sust.
m.
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Geom.
Definición:Cada una de las líneas que forman o limitan un polígono (DLE).Ejemplo(s):
|
|
4. sust.
m.
1ª datación del corpus: Aurel, Arithmética algebrática, 1552.
Marca diatécnica:
Geom.
Definición:Cada una de las superficies que forman o limitan un poliedro. (DLE, s. v. cara).Ejemplo(s):
|
|
5. sust.
m.
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:Generatriz de la superficie lateral del cono y del cilindro. (DLE).Ejemplo(s):
|
|
6. sust.
m.
1ª datación del corpus: Aurel, Arithmética algebrática, 1552.
Marca diatécnica:
Álg.
Definición:Cada uno de los valores que puede tener la incógnita de una ecuación. (x) (DRAE, s. v. raíz ).Ejemplo(s):
Información enciclopédica:En este problema, de construcción geométrica, cada uno de los lados desconocidos se pueden expresar como una raíz de una ecuación cuadrática con coeficientes numéricos conocidos, y esta raíz es, según Boyer (2003: 354), constructible geométricamente por medio de artificios conocidos de los Elementos de Euclides o del Álgebra de al-Kwārizmī, en el que cada uno de los lados se designan como “cosa” y entonces se resuelve el problema por la regla de la cosa y el “cuadrado”, por medio de una ecuación de segundo grado. Destacan Paradís y Malet (1989: 68) la presencia de esta clasificación en obras árabes, como la de Al Aamoulí, en la que los autores “hacían la siguiente aclaración de la notación utilizada: La cantidad que se multiplica por ella misma se llama raíz en aritmética, lado en geometría y shai’ (cosa) en álgebra; el resultado se llama entonces cuadrado”. |
|
7. sust.
m.
1ª datación del corpus: Medina, Regimiento de navegación, 1563.
Marca diatécnica:
Mar.
Definición:Cada uno de los costados de un navío por la parte de fuera.Ejemplo(s):
|
|
~ derecho del Sol
1ª datación del corpus: Anónimo, Repertorio tiempos, 1554.
Marca diatécnica:
Astr.
Definición:Hemisferio Norte.Ejemplo(s):
|
|
~ izquierdo del Sol
1ª datación del corpus: Anónimo, Repertorio tiempos, 1554.
Marca diatécnica:
Astr.
Definición:Hemisferio sur.Ejemplo(s):
|
|
dar ~
1ª datación del corpus: García de Palacio, Instrución náuthica, 1587.
Marca diatécnica:
Mar.
Definición:Reparar o componer el casco de la nave. (DLE, s.v. carenar).Ejemplo(s):
|
<< Volver