<< Volver
<< Volver
comprenso
Variantes:
comprehenso.
(
tomado del lat.
comprehensus, -a, -um, pp. de comprehendĕre
).
Familia léxica: aprender, aprendiz, comprender, comprendido, comprensión, deprender, emprender, incomprensible.
|
1. adj.
1ª datación del corpus: Chaves, Sacrobosco, Sphera, 1545.
Marca diatécnica:
Geom.
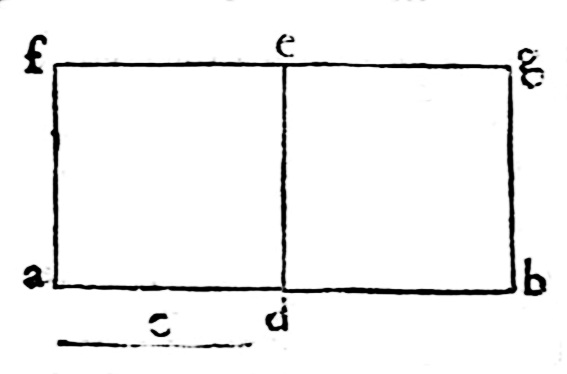
Definición:Inscrito, comprendido entre algunas líneas o superficies.Ejemplo(s):
|
<< Volver