ángulo
|
1. sust.
m.
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Geom.
Definición:Figura geométrica formada en una superficie por dos líneas que parten de un mismo punto; o también la formada en el espacio por dos superficies que parten de una misma línea. (DRAE 2001).Ejemplo(s):
|
|
2. sust.
m.
1ª datación del corpus: Loçano, Alberto, Architectura, 1582.
Marca diatécnica:
Arq.
Definición:Lugar de intersección de dos paredes o superficies vistas por su parte exterior. (Diccionario Histórico).Ejemplo(s):
|
|
3. sust.
m.
1ª datación del corpus: Chaves, Sacrobosco, Sphera, 1545.
Marca diatécnica:
Astr.
Definición:Cada una de las cuatro casas celestes correspondientes a los cuatro puntos cardinales (Diccionario Histórico).Ejemplo(s):
|
|
~ acuto
1ª datación del corpus: Pérez de Moya, Arithmética práctica, 1562.
Marca diatécnica:
Geom.
Definición:El menor o más cerrado que el recto. (DRAE, s. v. ~ agudo).Ejemplo(s):
|
|
~ agudo
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El menor o más cerrado que el recto. (DRAE 2001).Ejemplo(s):
|
|
~ circular
1ª datación del corpus: Molina Cano, Descubrimientos geométricos, 1598.
Marca diatécnica:
Geom.
Definición:El que se origina en la circunferencia del círculo con los extremos de sus diámetros y semidiámetros.Ejemplo(s):
|
|
~ contingente
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El formado por una recta y una curva o por dos curvas que sólo se encuentran en un punto. (Rodríguez Navas 1918, s. v. á. de contingencia).Ejemplo(s):
|
|
~ cuadrado
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Geom.
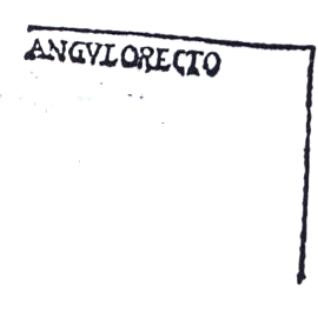
Definición:El que forman dos líneas, o dos planos, que se cortan perpendicularmente y equivale a 90°. (DRAE, s. v.ángulo recto).Ejemplo(s):
|
|
~ curvilíneo
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El que forman dos líneas curvas. (DRAE, s. v. ángulo curvilíneo).Ejemplo(s):
|
|
~ deinceps
1ª datación del corpus: Rojas, Teórica fortificación, 1598.
Marca diatécnica:
Geom.
Definición:Ángulo que falta a otro para componer dos rectos. (DRAE, ángulo suplementario).Ejemplo(s):
|
|
~ de (la) contingencia
1ª datación del corpus: Núñez, Álgebra en Arithmética, 1567.
Marca diatécnica:
Geom.
Definición:El formado por una recta y una curva o por dos curvas que sólo se encuentran en un punto. (Rodríguez Navas ).Ejemplo(s):
|
|
~ de la incidencia
1ª datación del corpus: Santa Cruz, Libro de las longitúdines, ca. 1567.
Marca diatécnica:
Ópt.
Definición:El formado por una trayectoria con la normal a la superficie de un medio, en el punto en el que lo encuentra. (DRAE, s. v. ángulo de incidencia).Ejemplo(s):
Información enciclopédica:En la óptica es el que forma por ejemplo el rayo de incidencia con el plano, y está de la parte del luminar, que envía el rayo. Fr. Angle d’incidence. Lat. Angulus incidenciae: es axioma admitido como cierto en Óptica y Geometría que el ángulo de incidencia es igual al de reflexión (Terreros: s. v. ángulo de incidencia). |
|
~ de posición
1ª datación del corpus: Santa Cruz, Libro de las longitúdines, ca. 1567.
Marca diatécnica:
Cosmogr.
Definición:El que forma el vertical que pasa por el cénit de dos lugares con el meridiano de uno de ellos (Autoridades).Ejemplo(s):
|
|
de reflexión
1ª datación del corpus: Ondériz, Euclides, Perspectiva y especularia, 1584-85.
Marca diatécnica:
Ópt.
Definición:El formado por la normal a una superficie y el rayo reflejado en ella. (DRAE 2001).Ejemplo(s):
|
|
~ de sección
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:Parte del círculo comprendida entre un arco y su cuerda.Ejemplo(s):
|
|
~ de semicírculo
1ª datación del corpus: Núñez, Álgebra en Arithmética, 1567.
Marca diatécnica:
Geom.
Definición:El que forma un diámetro con la circunferencia a la que pertenece. (Ortiz 2000: 217, en nota).Ejemplo(s):
|
|
~ derecho
1ª datación del corpus: Santa Cruz, Libro de las longitúdines, ca. 1567.
Marca diatécnica:
Geom.
Definición:El que forman dos líneas, o dos planos, que se cortan perpendicularmente y equivale a 90°. (DRAE, s. v. ángulo recto).Ejemplo(s):
|
|
~ en el centro del círculo
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El que forman dos líneas rectas tiradas desde el centro de un círculo hasta su circunferencia. (Autoridades, s. v. ángulo en el centro).Ejemplo(s):
|
|
~ en la circunferencia
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El que se forma por dos líneas rectas, que concurren en la circunferencia de un círculo, que cortándole van a terminarse en otros dos puntos de la misma circunferencia. (Autoridades, s.v. ángulo en la circunferencia).Ejemplo(s):
|
|
~ esferal
1ª datación del corpus: Chaves, Sacrobosco, Sphera, 1545.
Marca diatécnica:
Geom.
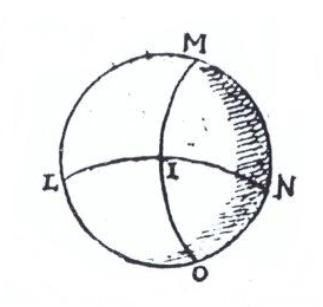
Definición:El que se forma en la superficie de la esfera en el concurso de dos circunferencias de círculos máximos que se cortan. (Autoridades, s. v. ángulo esférico).Ejemplo(s):
|
|
~ esférico
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El que se forma en la superficie de la esfera en el concurso de dos circunferencias de círculos máximos que se cortan. (Autoridades, s. v. ángulo esférico).Ejemplo(s):
|
|
~ exterior
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Geom.
Definición:El formado por un lado de un polígono y la prolongación del contiguo. (DRAE, s. v. ángulo externo).Ejemplo(s):
|
|
~ extrínseco
1ª datación del corpus: Ondériz, Euclides, Perspectiva y especularia, 1584-85.
Marca diatécnica:
Geom.
Definición:El formado por un lado de un polígono y la prolongación del contiguo. (DRAE, s. v. ángulo externo).Ejemplo(s):
|
|
~ interior
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Geom.
Definición:El formado por los lados contiguos de un polígono, hacia el interior de este. (DRAE, s. v. ángulo interno).Ejemplo(s):
|
|
~ intrínseco
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El formado por los lados contiguos de un polígono, hacia el interior de este. (DRAE, s. v. ángulo interno).Ejemplo(s):
|
|
~ llano
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El formado por dos líneas contenidas en el mismo plano. (DRAE, s. v. ángulo plano).Ejemplo(s):
|
|
~ mezclado
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El que forman una recta y una curva. (DRAE, s. v. ángulo mixto).Ejemplo(s):
|
|
~ mixto
1ª datación del corpus: Martínez de Aranda, Zerramientos montea, ca. 1599.
Marca diatécnica:
Geom.
Definición:El que forman una recta y una curva. (DRAE 2001).Ejemplo(s):
|
|
~ obtuso
1ª datación del corpus: Pérez de Moya, Arithmética práctica, 1562.
Marca diatécnica:
Geom.
Definición:El mayor o más abierto que el recto. (DRAE 2001).Ejemplo(s):
|
|
~ ortogonal
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Geom.
Definición:El que forman dos líneas, o dos planos, que se cortan perpendicularmente y equivale a 90°. (DRAE, s. v. ángulo recto).Ejemplo(s):
|
|
~ plano
1ª datación del corpus: Álaba, Perfeto capitán, 1590.
Marca diatécnica:
Geom.
Definición:El formado por dos líneas contenidas en el mismo plano. (DRAE 2001).Ejemplo(s):
|
|
~ rectángulo
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Geom.
Definición:El que forman dos líneas, o dos planos, que se cortan perpendicularmente y equivale a 90°. (DRAE, s. v. ángulo recto).Ejemplo(s):
|
|
~ rectilíneo
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El que se forma de dos líneas rectas. (Autoridades).Ejemplo(s):
|
|
~ recto
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553 .
Marca diatécnica:
Geom.
Definición:El que forman dos líneas, o dos planos, que se cortan perpendicularmente y equivale a 90°. (DRAE 2001).Sinónimos(s):ángulo cuadrado, ángulo derecho, ángulo ortogonal, ángulo rectángulo, derecho5, recto4.Ejemplo(s):
|
|
~ romo
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El mayor o más abierto que el recto. (DRAE, s. v. ángulo obtuso).Ejemplo(s):
|
|
~ semirrecto
1ª datación del corpus: Álaba, Perfeto capitán, 1590.
Marca diatécnica:
Geom.
Definición:El de 45º, mitad del recto. (DRAE 2001).Ejemplo(s):
|
|
~ sólido
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
Definición:El que se hace por más de dos ángulos planos, que no están en una misma superficie plana, y concurren en un mismo punto. (Autoridades).Ejemplo(s):
|
|
~s alternos
1ª datación del corpus: Ondériz, Euclides, Perspectiva y especularia, 1584-85.
Marca diatécnica:
Geom.
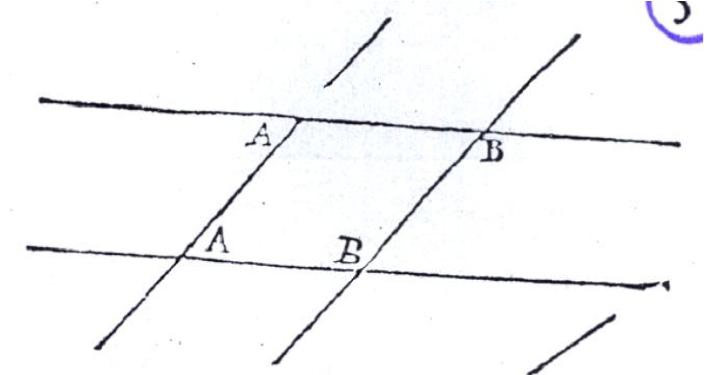
Definición:Los dos que, sin ser adyacentes, se forman a distinto lado de una recta que corta a otras dos. (DRAE 2001).Ejemplo(s):
|
|
~s colaterales
1ª datación del corpus: Molina Cano, Descubrimientos geométricos, 1598.
Marca diatécnica:
Geom.
Definición:Los formados a un mismo lado de una línea recta por otra que la corta. (DRAE, s. v. ángulos adyacentes).Ejemplo(s):
|
|
~s contrapuestos
1ª datación del corpus: Núñez, Álgebra en Arithmética, 1567.
Marca diatécnica:
Geom.
Definición:Los que tienen el vértice común y los lados de cada uno en prolongación de los del otro. (DRAE, s. v. ángulos opuestos por el vértice).Ejemplo(s):
|
|
~s de advértice
1ª datación del corpus: Rojas, Teórica fortificación, 1598.
Marca diatécnica:
Geom.
Definición:Los que tienen el vértice común y los lados de cada uno en prolongación de los del otro. (DRAE, s. v. ángulos opuestos por el vértice).Ejemplo(s):
|
|
~s opósitos
1ª datación del corpus: Pérez de Moya, Arithmética práctica, 1562.
Marca diatécnica:
Geom.
Definición:Los que están formados por dos rectas, que se cortan en un punto. (Gaspar y Roig, 1855, s. v. opuesto).Ejemplo(s):
|
|
~s opuestos en la vértice
1ª datación del corpus: Ondériz, Euclides, Perspectiva y especularia, 1584-85.
Marca diatécnica:
Geom.
Definición:Los que tienen el vértice común y los lados de cada uno en prolongación de los del otro. (DRAE, s. v. ángulos opuestos por el vértice).Ejemplo(s):
|
|
en ~
1ª datación del corpus: Loçano, Alberto, Architectura, 1582.
Marca diatécnica:
Geom.
Definición:Formando un ángulo. (Diccionario Histórico).Ejemplo(s):
|
|
en ~ oblicuo
1ª datación del corpus: García de Céspedes, Instrumentos nuevos, 1606.
Marca diatécnica:
Geom.
Definición:En posición oblicua.Ejemplo(s):
|
<< Volver