reducir
|
1. v. tr.
1ª datación del corpus: Girava, Fineo, Geometría práctica, 1553.
Marca diatécnica:
Geom.
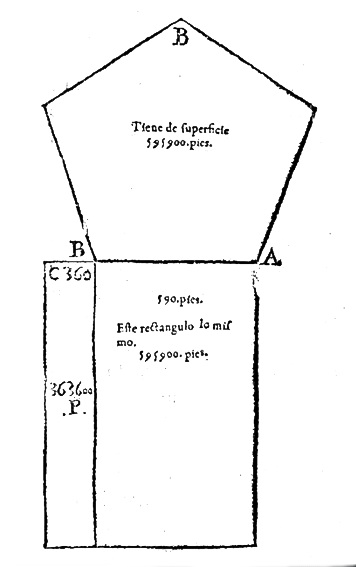
Definición:Convertir, transformar una figura geométrica en otra equivalente.Ejemplo(s):
|
|
2. v. tr. / u. t. c. intr.
1ª datación del corpus: Cortés de Albacar, Breve compendio sphera, 1556.
Marca diatécnica:
Cart.
Definición:Expresar en el mapa el valor de una cantidad en unidades de especie distinta de la dada.Ejemplo(s):
|
|
3. v. tr. / u. t. c. intr.
1ª datación del corpus: Cortés de Albacar, Breve compendio sphera, 1556.
Marca diatécnica:
Cart.
Definición:Transfomar un mapa a un punto o escala diferente del que se aplica al modelo.Ejemplo(s):
|
|
4. v. tr.
u. t. c. prnl.
1ª datación del corpus: Ortega, Conpusición Arismética y Geometría, 1512.
Marca diatécnica:
Arit.
Definición:Convertir un número en otro equivalente, principalmente, un entero en un quebrado.Ejemplo(s):
|
|
5. v. tr.
1ª datación del corpus: Aurel, Arithmética algebrática, 1552. Definición:Cambiar o trocar una moneda por otra. (Autoridades).Ejemplo(s):
|
|
6. v. tr.
1ª datación del corpus: Pérez Vargas, De re metallica, 1568.
Marca diatécnica:
Metal.
Definición:Apurar un metal hasta conseguir la ley deseada.Ejemplo(s):
|
|
~ a cuerpo
1ª datación del corpus: Alonso Barba, Arte de los metales, 1640.
Marca diatécnica:
Metal.
Definición:Espesarse, condensarse, solidificarse un metal.Ejemplo(s):
|
<< Volver