<< Volver
<< Volver
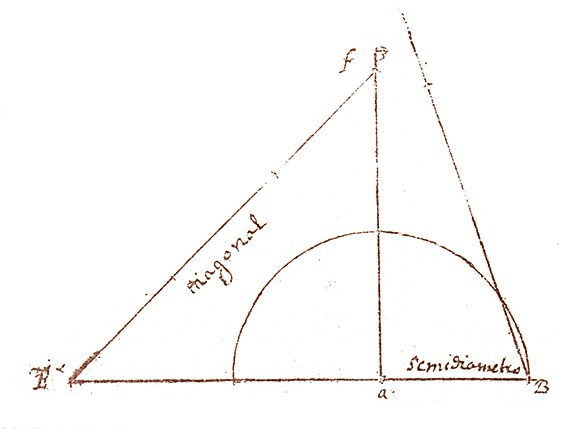
diagonal
(
tomado del lat.
dĭăgōnālis 'íd.'
(Lewis-Short)
).
Familia léxica: ambligonio, centágono, cincuentágono, decágono, diagonalmente, diagonio, diágono, dodecágono, heptágono, hexagonal, hexagónico, hexágono, isogonio, nonágono, octógono, ortogonal, ortogonalmente, ortogónicamente, ortogonio, ortógono, oxigonio, pentágono, poligónico, poligonio, polígono, septágono, sexágono, tetragónico, tetrágono, trigonio, trígono, veintágono, veinticincágono.
|
1. adj.
u. t. c. sust.
1ª datación del corpus: Sagredo, Medidas Romano, 1526.
Marca diatécnica:
Geom.
Definición:Dicho de una línea recta: que en un polígono va de un vértice a otro no inmediato, y en un poliedro une dos vértices cualesquiera no situados en la misma cara. (DRAE 2001).Ejemplo(s):
|
|
2. sust.
f.
1ª datación del corpus: López de Arenas, Reglas de la carpintería, 1619.
Marca diatécnica:
Geom.
Definición:Lado opuesto al ángulo recto en un triángulo rectángulo. (DLE, s. v. hipotenusa).Ejemplo(s):
|
|
Véase arco ~
|
|
Véase línea ~.
|
|
Véase raya ~.
|
<< Volver